2023年度岩手県公立高校入試問題
【数学】大問12
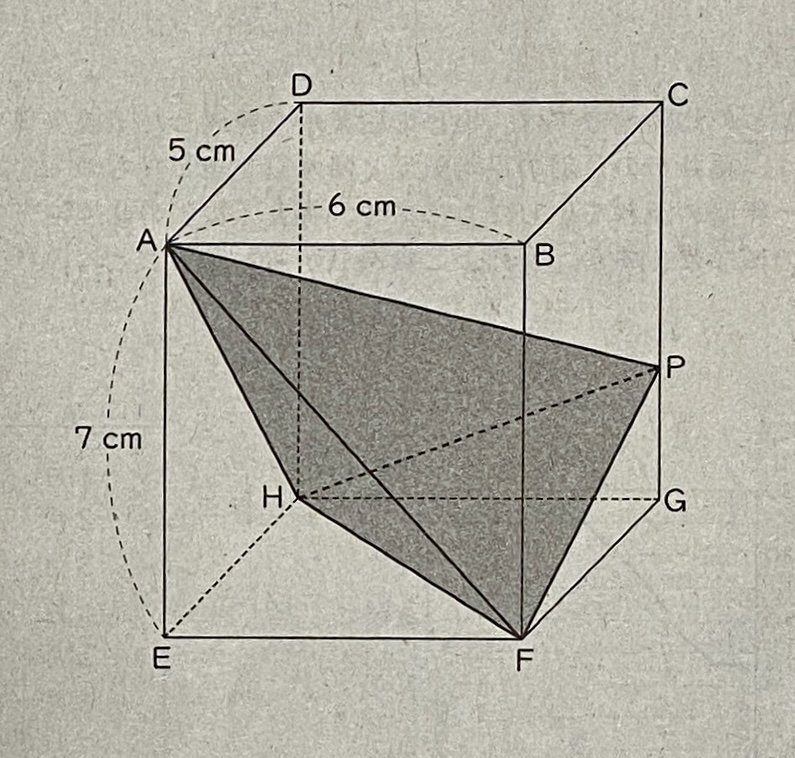
下の図は、AB = 6cm, AD = 5cm, AE = 7cmの直方体ABCD-EFGHです。
このとき、次の(1)(2)の問いに答えなさい。
(1)線分AFの長さを求めなさい。
(2) CG上にPG=2cmとなるような点Pをとったとき、四面体AHFPの体積を求めなさい。
単元:中1 空間図形/中3 三平方の定理
内容:線分の長さと立体の体積を求める
(1)は長方形の対角線の長さを三平方の定理を用いて解きます。
公式に当てはめれば正解できる教科書の例題レベルの問題です。
(解き方は省略します)
(2)はいきなり応用問題になります。今回の高校入試でも一番難しい問題だと思います。
しかし、実際には合否には直接関係ない問題になります。
なぜなら、受験生の7割くらいの生徒は難しすぎて最初から捨てる問題、あるいは、解く学力がある生徒でも時間内に解くのは困難な問題だからです。
それでも、あえて注目すべき問題としたのは、図形の見方は感覚に頼る部分が大きいので、さまざまな問題を解くことで図形感覚を養ってほしいという理由からです。
実際の入試では解かない問題であっても解き方をきちんと理解しておくことは重要です。
それでは、解説をしていきます。
解き方ですが、最初は図形の体積を直接求めることができるかを確認します。
試してみましたが、計算して求められる数字が複雑なので、体積を直接求めるのは難しいと判断しました。
そこで、別の解き方を考えることにします。
ということで、「直方体の体積」から「求める体積以外の空間の体積」を引いて求めます。
中学校で習っている体積の求め方は、柱体と錐体と球しかありません。高校入試では錐体の体積を求めることが多いことを考えると、直方体の中に錐体を見つけられるかがポイントになります。
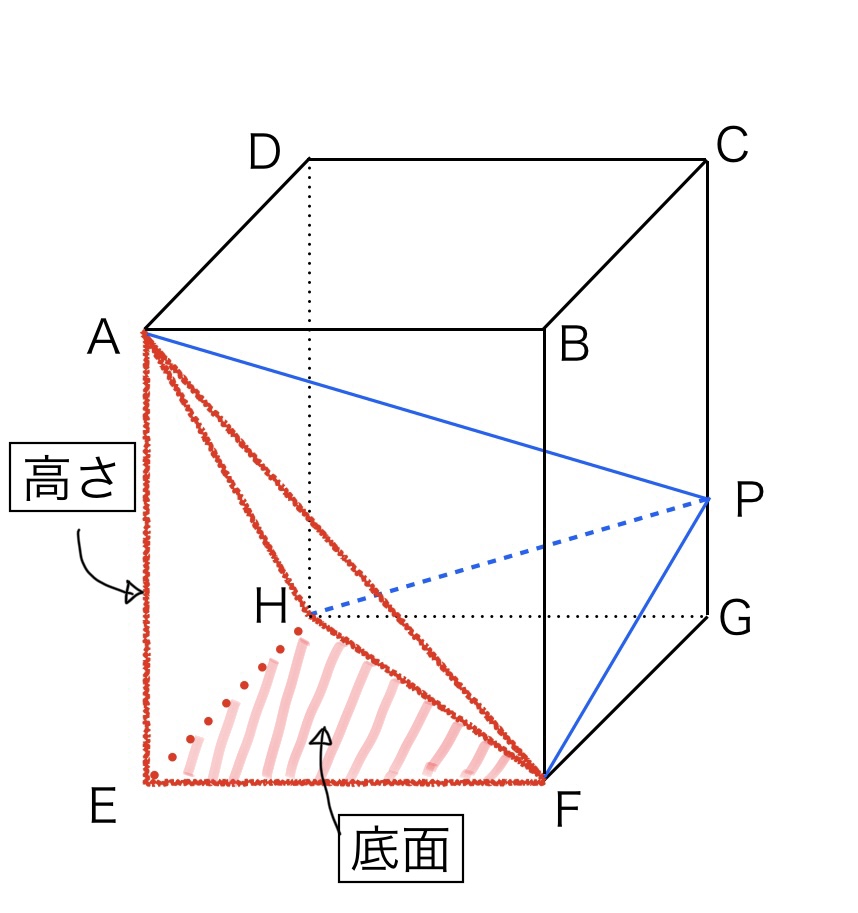
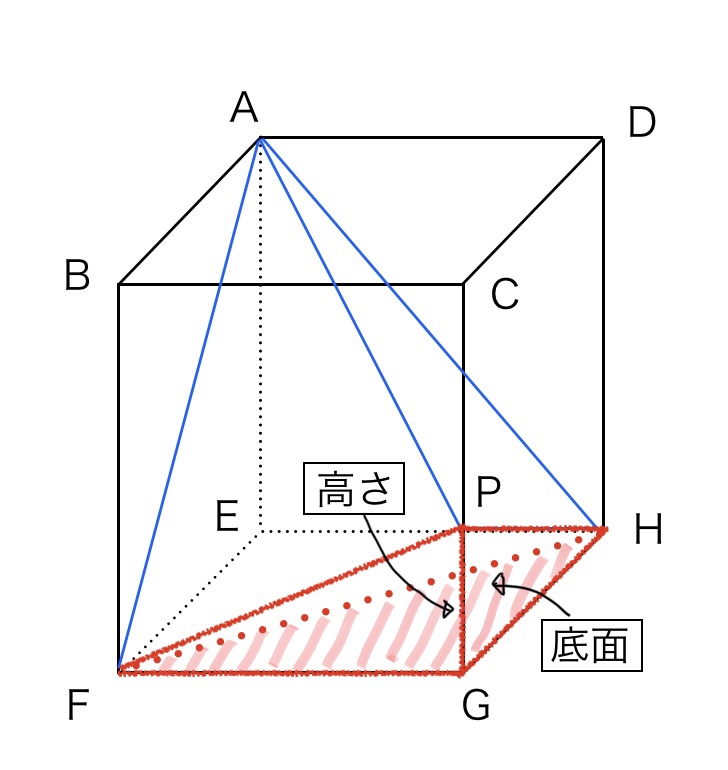
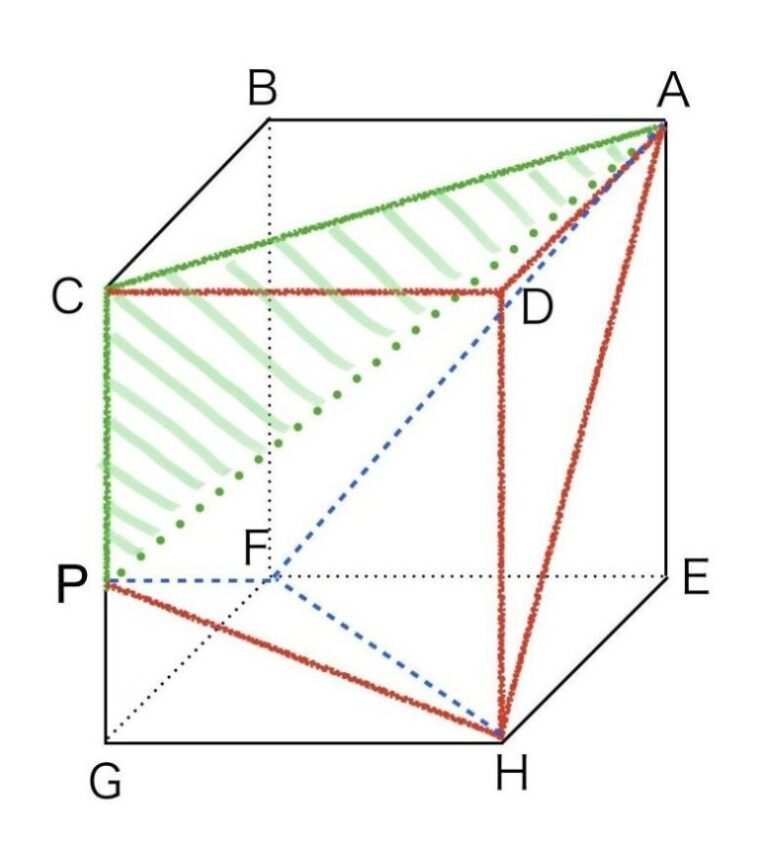
左図は設問の図と同じ向きで、右図は直方体の右側面を正面に回転させた図です。
赤線で囲んだ三角錐の体積をそれぞれ求めていきます。
左図では面EFHが底面で高さが線分AEになるので、体積①(左上の図)=35㎠
右図では面FGHが底面で高さが線分PGになるので、体積②(右上の図)=10㎠
次に、残りの体積を取り出すと、下の図のようになります。
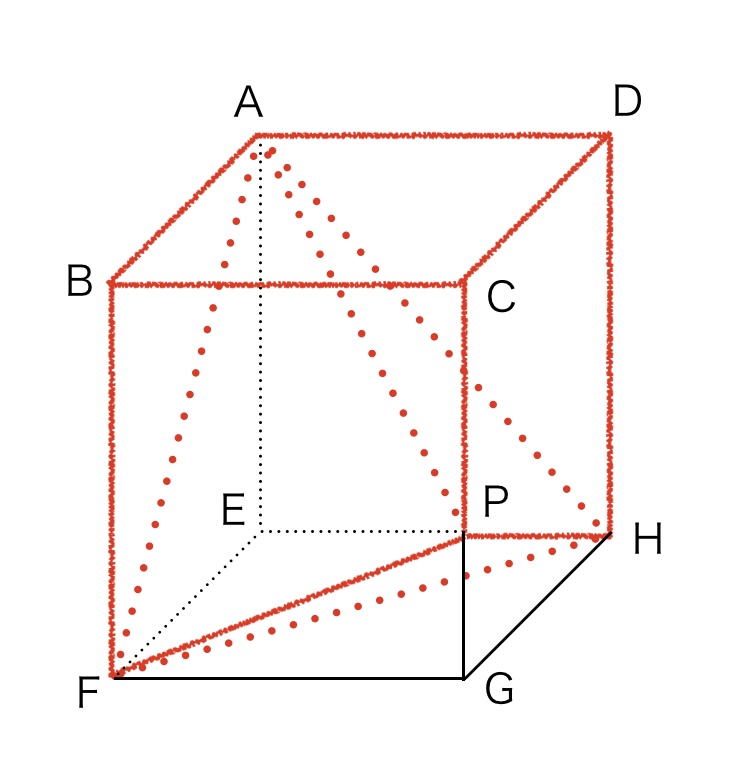
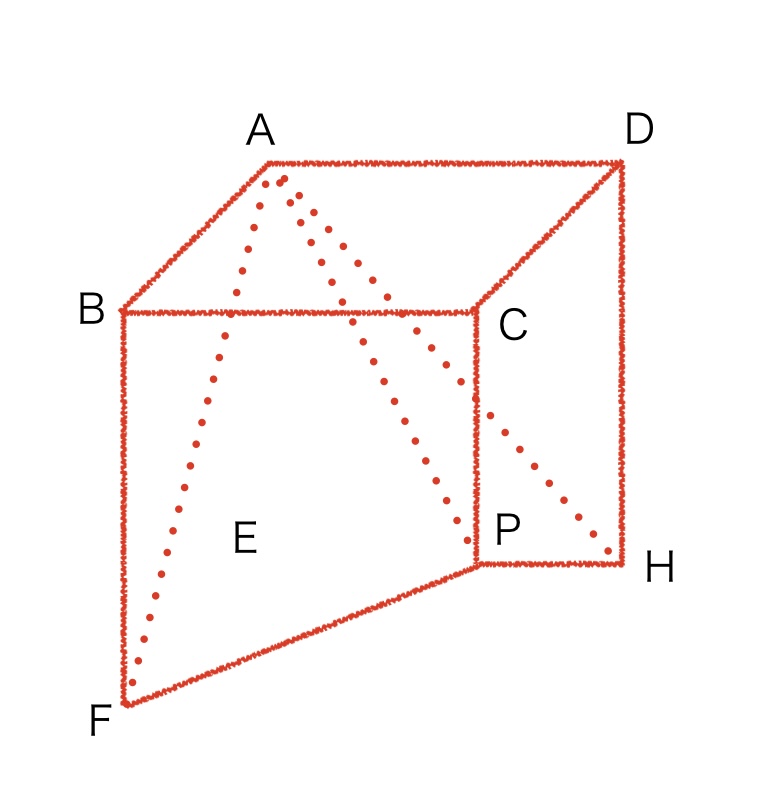
右上の図の形では、錐体にならないので、体積を求めることができません。
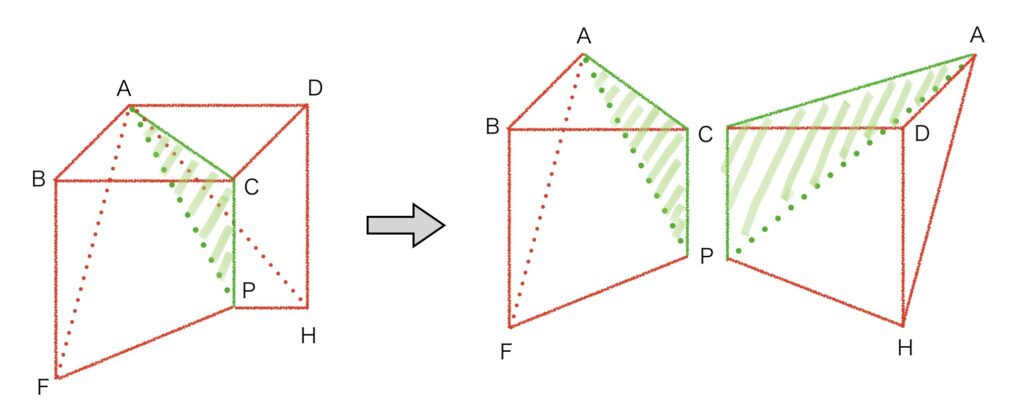
そこで、設問の図にはないところで分割してみました。少し分かりにくいかもしれませんが、面CPAで分割しました。
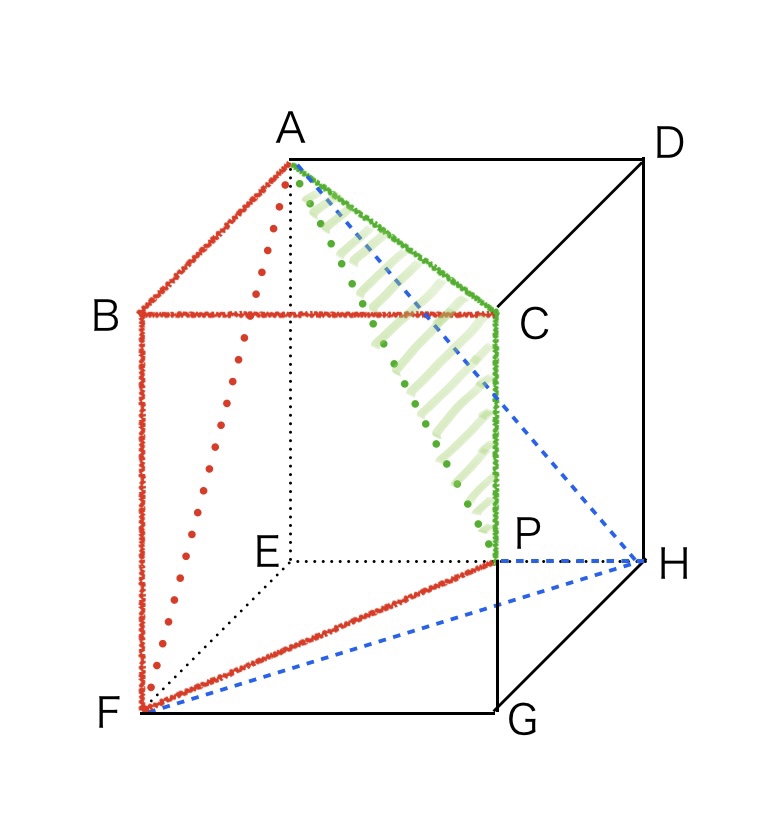
2つに分割したうちの左側の図形を元の立方体における位置を示したのが左上の図で、
右上の図は図形を見やすくするために抜き出したものです。
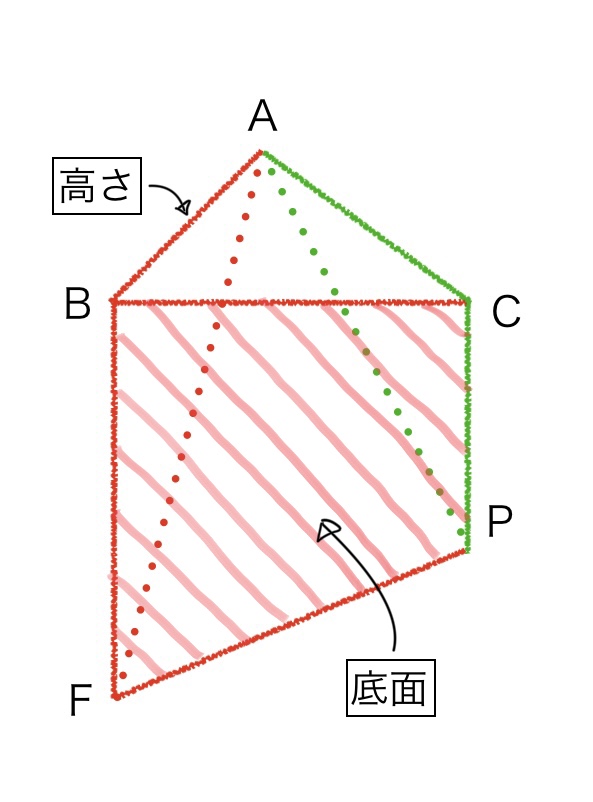
底面がBF//CPの台形BFPCで、高さが線分ABの四角錐になるので、体積③(右上の図)=60㎠
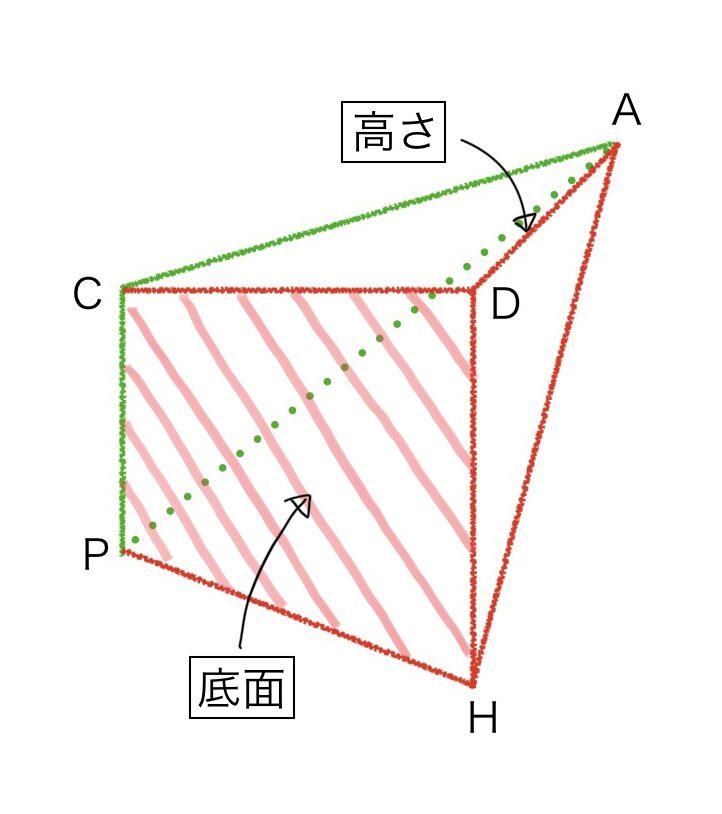
同様に、2つに分割したうちの右側の図形を元の立方体における位置を示したのが左上の図で、
右上の図は図形を見やすくするために抜き出したものです。
底面がDH//CPの台形DHPCで、高さが線分ADの四角錐になるので、体積④(右上の図)=60㎠
以上から、求める体積
=直方体−(体積①+体積②+体積③+体積④)
=210−(35+10+60+60)
=45㎠
なんとか求められましたね。
図形の問題は、試行錯誤する中で、一瞬のひらめきによって正解までたどり着けるのがおもしろいところです。
ぜひ、いろいろな図形問題にチャレンジしてみてください。

