【数学】2023年岩手県公立高校入試「差がついた問題」

昨年度から岩手県教育委員会によって岩手県公立高校入試の分析結果が公表されるようになりました。

その分析結果から上位層と中上位層で「差がついた問題」に注目して解説していきます。

まずは2023年岩手県公立高校入試の数学全体の結果です。

S層は入試得点が76点〜100点の上位層。
R層は入試得点が51点〜75点の中上位層。

S層(上位層)とR層(中上位層)の正答率の比較

大問	小問	S層正答率(%)	R層正答率(%)	差(S−R)
1	(1)	100	99	1
1	(2)	100	87	13
1	(3)	100	87	13
1	(4)	100	98	2
1	(5)	100	99	1
2		96	65	31
3		96	88	8
4	(1)	98	92	6
4	(2)	98	64	34
4	(3)	89	50	39
5		78	45	33
6		79	49	30
7	(1)	98	96	2
7	(2)	98	91	7
8		97	91	6
9		84	44	40
10	(1)	79	33	46
10	(1)	93	44	49
10	(2)	42	2	40
11	(1)	96	78	18
11	(2)	41	6	35
12	(1)	95	87	8
12	(2)	2	0	2

2023年度岩手県公立高校入試結果（S層正答率とR層正答率の差）

下の2つのグラフはS層(上位層)とR層(中上位層)の正答率を比較したものです。

1つ目のグラフ…大問1から大問4までの比較

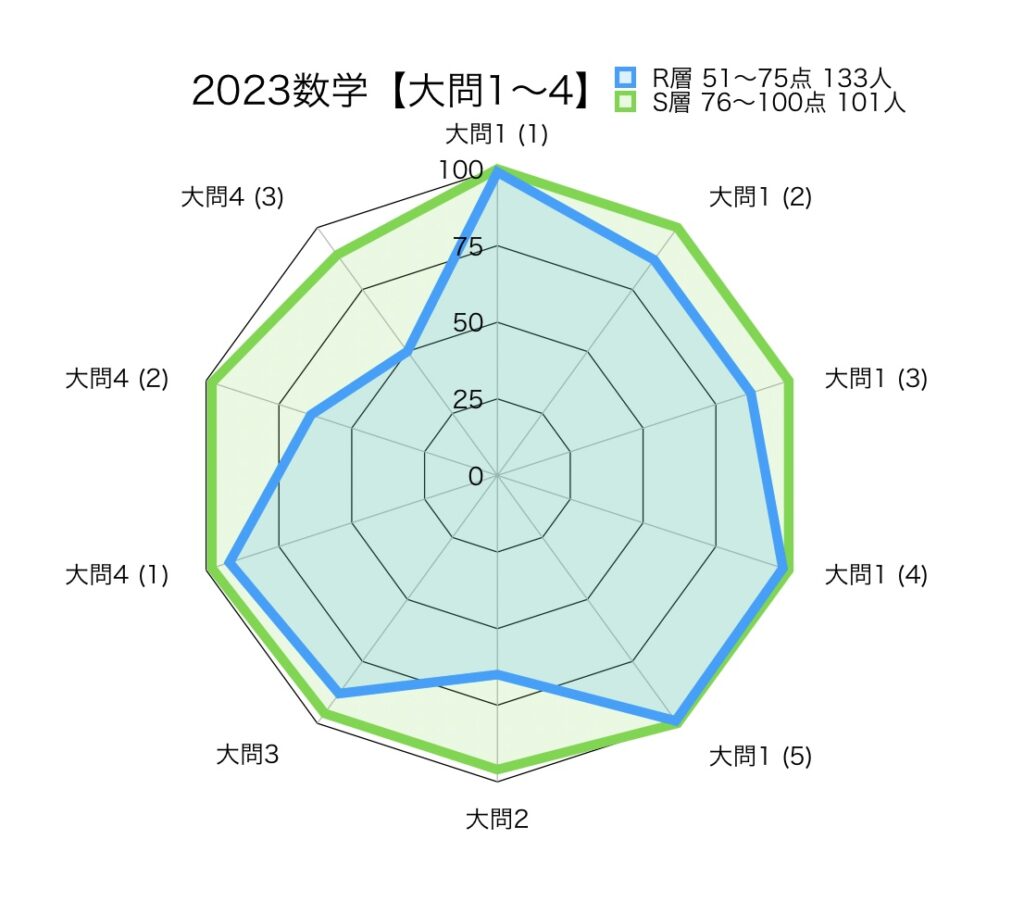
すべての問題が基本問題です。

上位層のS層はほぼ満点です。

中上位層のR層はところどころ取りこぼしがあります。

2つ目のグラフ…大問5から大問12までの比較

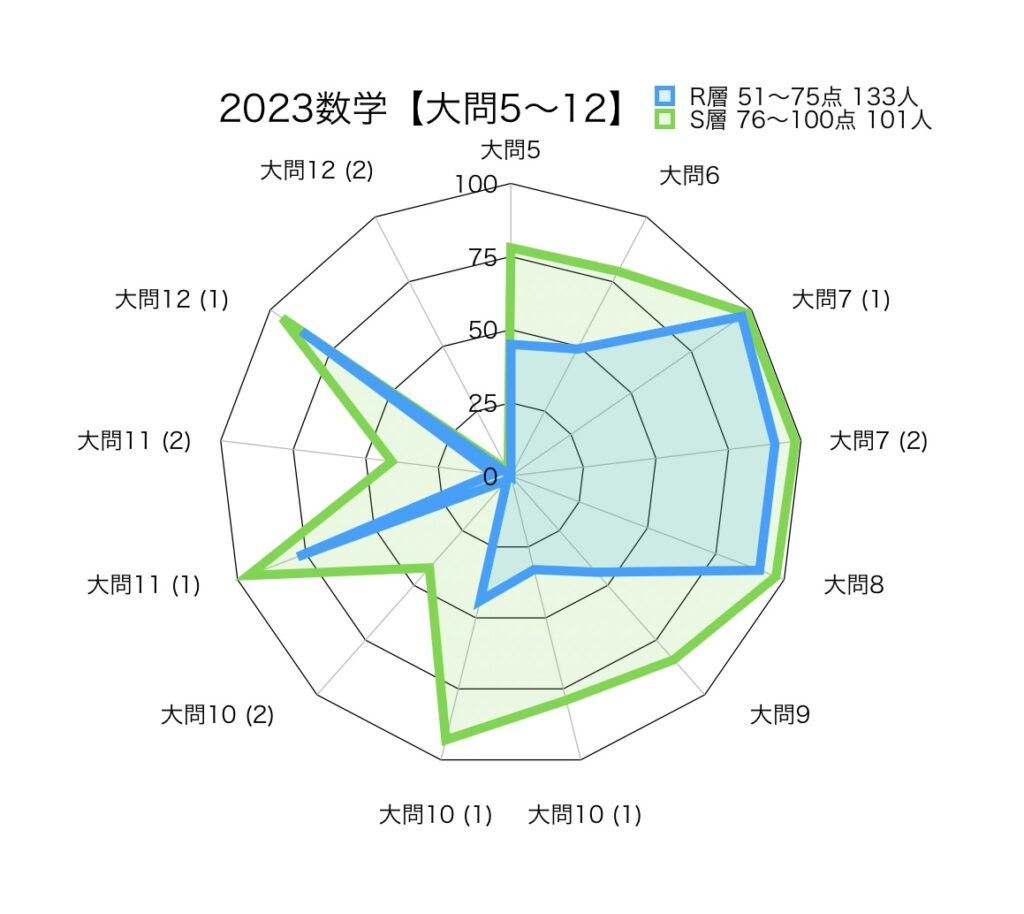
基本問題(大問5〜8、11(1)、12(1))と応用問題(大問9、10、11(2)、12(2))が混在しています。

上位層のS層は、大問10、11(2)、12(2)以外はきちんと得点できています。

中上位層のR層は、応用問題を解く時間が足りない、あるいは、最初から応用問題を解かないという生徒が多いと推測しています。

それでは、ここから上位層と中上位層で「差がついた問題」を解説していきます。

S層（上位層）内で差がついた問題

◉応用：大問10(2) 1次関数、動く図形の変化(S層正答率42%)

1次関数は中2の範囲ですが、中3の教科書(東書)のy＝x²の単元に類似問題があるので、きちんと練習した人は正解できたのではないでしょうか。時間の経過とともに図形の状態を考察する必要があるので、なかなか理解しづらいところがあります。図形を動かしてどう変化するかを一度、自分でやってみると理解できると思います。

2023年3月岩手県公立高校入試　注目すべき問題【数学大問10】

2023年度岩手県公立高校入試問題　【数学】大問10次の図Ⅰは、荷物検査場のようすを真上から見たものです。スーツケースなどの荷物は、ベルトコンベアに載せられ、矢...

◉応用：大問11(2) y=x²のグラフ、面積が等しい(S層正答率41%)

中３の範囲です。y＝x²のグラフ上で面積が同じ2つの三角形を作る時の点の座標を求める問題です。y＝x²の応用問題としては典型的な問題なので、他のパターンの問題を含めて、理解と演習をすればしっかり得点できると思います。

S層（上位層）とR層（中上位層）で差がついた問題

基本問題編

	大問	小問	R層正答率	S層正答率	差(S−R)
①	2	–	65%	96%	31	文字と式
②	4	2	64%	98%	34	平面図形
③	4	3	50％	89％	39	平面図形
④	5	−	45％	78％	33	作図
⑤	6	−	49％	79％	30	箱ひげ図